From Faraday's Law
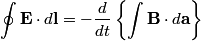 If 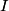 is the current and Unparseable_latex_formula\Omega is the current and Unparseable_latex_formula\Omega is the resistance of the wire loop, then is the resistance of the wire loop, then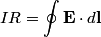 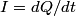 , so , so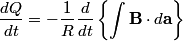 We integrate both sides with respect to time to obtain the amount of charge that flows past a given point in the wire: 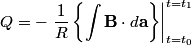 where 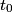 is some time before the wire loop was pulled out of the magnetic field and is some time before the wire loop was pulled out of the magnetic field and 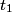 is sometime after. At is sometime after. At 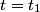 , there is no magnetic flux through the loop, and at , there is no magnetic flux through the loop, and at 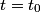 , the magnetic flux through the loop is , the magnetic flux through the loop is 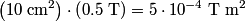 . So, . So,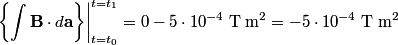 So, 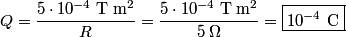 Therefore, answer (A) is correct. |